Coordenadas Cartesianas

Son un ejemplo de coordenadas ortogonales usadas en espacios euclídeos caracterizadas por la existencia de dos ejes perpendiculares entre sí que se cortan en un punto origen. Las coordenadas cartesianas se definen como la distancia al origen de las proyecciones ortogonales de un punto dado sobre cada no de los ejes.

Un punto cualquiera de una recta puede asociarse y representarse con un número real, positivo si está situado a la derecha de un punto O, y negativo si está a la izquierda. Dicho punto se llama origen de coordenadas O (letra O) y se asocia al valor 0 (cero).

Corresponde a la dimensión uno, que se representa con el eje X, en el cual se define un origen de coordenadas, simbolizado con la letra O (O de origen) y un vector unitario en el sentido positivo de las x: .

Este sistema de coordenadas es un espacio vectorial de dimensión uno, y se le pueden aplicar todas las operaciones correspondientes a espacios vectoriales. También se le llama recta real.

Un punto:

también puede representarse:

La distancia entre dos puntos A y B es:

Plano euclídeo

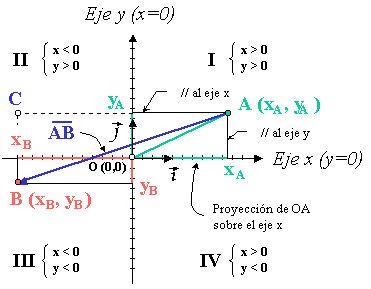
Con un sistema de referencia conformado por dos rectas perpendiculares que se cortan en el origen, cada punto del plano puede "nombrarse" mediante dos números: (x, y), que son las coordenadas del punto, llamadas abscisa y ordenada, respectivamente, que son las distancias ortogonaldes de dicho punto respecto a los ejes cartesianos.

Sistema de coordenadas cartesianas.

La ecuación del eje x es y = 0, y la del eje y es x = 0, rectas que se cortan en el origen O, cuyas coordenadas son, obviamente, (0, 0).

Se denomina también eje de las abscisas al eje x, y eje de las ordenadas al eje y. Los ejes dividen el espacio en cuatro cuadrantes en los que los signos de las coordenadas alternan de positivo a negativo (por ejemplo, las dos coordenadas del punto A serán positivas, mientras que las del punto B serán ambas negativas).

Las coordenadas de un punto cualquiera vendrán dadas por las proyecciones del segmento entre el origen y el punto sobre cada uno de los ejes.

Sobre cada uno de los ejes se definen vectores unitarios (i y j) como aquellos paralelos a los ejes y de módulo (longitud) la unidad. En forma vectorial, la posición del punto A se define respecto del origen con las componentes del vector OA.

La posición del punto A será:

Nótese que la lista de coordenadas puede expresar tanto la posición de un punto como las componentes de un vector en notación matricial.

La distancia entre dos puntos cualesquiera vendrá dada por la expresión:

Aplicación del teorema de Pitágoras al triángulo rectángulo ABC.

Un vector cualquiera AB se definirá restando, coordenada a coordenada, las del punto de origen de las del punto de destino:

Evidentemente, el módulo del vector AB será la distancia d_AB entre los puntos A y B antes calculada.

Espacio euclídeo

Si tenemos un sistema de referencia formado por tres rectas perpendiculares entre sí (X, Y, Z), que se cortan en el origen (0, 0, 0), cada punto del espacio puede nombrarse mediante tres números: (x, y, z), denominados coordenadas del punto, que son las distancias ortogonales a los tres planos principales: los que contienen las parejas de ejes YZ, XZ e YX, respectivamente.

coordenadas cartesianas espaciales.

Los planos de referencia XY (z = 0); XZ (y = 0); e YZ (x = 0) dividen el espacio en ocho cuadrantes en los que, como en el caso anterior, los signos de las coordenadas pueden ser positivos o negativos.

La generalización de las relaciones anteriores al caso espacial es inmediata considerando que ahora es necesaria una tercera coordenada (z) para definir la posición del punto.

Las coordenadas del punto A serán:

y el B:

La distancia entre los puntos A y B será:

El segmento AB será:

Cambio del sistema de coordenadas

Tanto en el caso plano como en el caso espacial pueden considerarse tres transformaciones elementales: traslación (del origen), rotación (alrededor de un eje) y escalado.

Traslación del origen

Traslación del origen en coordenadas cartesianas.

Suponiendo un sistema de coordenadas inicial S1 con origen en O y ejes x e y

y las coordenadas de un punto A dado, sean en el sistema S1:

dado un segundo sistema de referencia S2

Siendo los centros de coordenadas de los sistemas 0 y 0´, puntos distintos, y los ejes x, x´; e y, y´ paralelos dos a dos, y las coordenadas de O´, respecto a S1:

Se dice traslación del origen, a calcular las coordenadas de A en S2, según los datos anteriores, que llamaremos:

Dados los puntos O, O´ y A, tenemos la suma de vectores:

despejando

Lo que es lo mismo que:

Separando los vectores por coordenadas:

y ampliándolo a tres dimensiones:

Rotación alrededor del origen

Rotación alrededor del origen en coordenadas cartesianas.

Dado un sistema de coordenadas en el plano S₁ con origen en O y ejes x e y:

y una base ortonormal de este sistema:

Un punto A del plano se representará en este sistema según sus coordenadas:

Para un segundo sistema S₂ de referencia girado un ángulo , respecto al primero:

y con una base ortonormal:

Al cálculo de las coordenadas del punto A, respecto a este segundo sistema de referencia, girado respecto al primero, se llama rotación alrededor del origen, siendo su representación:

Hay que tener en cuenta que el punto y son el mismo punto, ; se emplea una denominación u otra para indicar el sistema de referencia empleado. El valor de las coordenadas respecto a uno u otro sistema, sí son diferentes, y es lo que se pretende calcular.

La representación de B₁ en B₂ es:

Dado que el punto A en B1 es:

con la transformación anterior tenemos:

Y, deshaciendo los paréntesis:

reordenando:

Como:

;

Tenemos que:

Como sabíamos:

Por identificación de términos:

Que son las coordenadas de A en B₂, en función de las coordenadas de A en B₁ y de .

[editar] Escalado

Sea un punto con coordenadas (x,y) en el plano. Si se cambia la escala de ambos ejes en un factor λ, las coordenadas de dicho punto en el nuevo sistema de coordenadas pasarán a ser:

El factor de escala λ no necesariamente debe ser el mismo para ambos ejes.

Cálculo matricial

Siendo [T] la matriz de transformación y cuyas filas son precisamente las componentes de los vectores unitarios i ' y j ' respecto de los originales i y j, o si se prefiere, cuyas columnas son las componentes de los vectores unitarios originales en el sistema de referencia rotado.